|
comme on est en régime stationnaire, Du/dt=u*du/dx, l'équation devient u*du/dx=nu*d²u/dy², avec u(x=0,y)=u0, u(x,y=0)=0. Malheureusement cette équation ne s'intègre pas aussi facilement, Blasius (1908) a obtenu une solution du type u(x,y)=u0*profil(z), avec z=y/racine(u0/(nu*x)), où la fonction profil ressemble à une fonction erf sans en être une, n'admet pas d'expression analytique mais seulement un développement en série tiré de l'équation différentielle 2F'''+F*F''=0 avec F(0)=F'(0)=0 et F(infini)=1 (équation de Blasius), où profil(z)=F'(z). pour avoir F(infini)=1, Blasius a posé F''(0)=A=0,332 ... Bref, les choses se compliquent vraiment et on préfère opter pour un modèle simplifié de la couche limite, où le profil des vitesses a été linéarisé selon y (voir plus bas ). La solution lagrangienne est néanmoins intéressante car on la retrouve aussi La table ci-dessous donne les valeurs des différentes diffusivités pour l'air et l'eau:
|
||||||||||||||||||||||||||||||||||||||||||||||
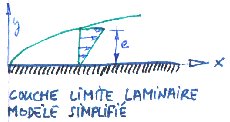 Voici
notre modèle simplifié de la couche limite, où la
description du profil des vitesses se ramène à un seul
paramètre,
l'épaisseur e de la couche. e dépend de x. A x
donné,
u(y)=u0*y/e
si y<e, u(y)=u0 si y>e.
Soit tau la contrainte de frottement à la paroi: tau=eta*(du/dy)y=0 (en Pa=N/m²). eta=rho*nu est la viscosité dynamique (en Pa.s), rho la masse volumique (kg/m3). On a donc tau=u0*eta/e. Le débit de quantité de mouvement déficitaire est P-=integrale[0,e](rho*u*(u0-u)*dy)=rho*u0²*integrale[0,e]((y/e-y²/e²)*dy), P-=rho*u0²*e/6, P-=Pdyn*e/3 (en N/m). Pdyn=rho*u0²/2 est la pression dynamique (surcroit de pression face à l'écoulement). L'augmentation de P- selon x est dûe au frottement: tau=d(P-)/dx, d'où l'on tire nu/e=u0*(de/dx)/6 puis d(e²)=12*nu*dx/u0 puis comme e(x=0)=0, e=2*racine(3*nu*x/u0). Par définition le nombre de Reynolds de l'écoulement est Re=u0*x/nu. On a donc e=2*x*racine(3/Re). Le coefficient de frottement Cf est défini par tau=Pdyn*Cf. Il s'agit du coefficient de frottement local, il est adimensionnel. On en tire u0*eta/e=(rho*u0²/2)*Cf, 2*nu/u0/e=Cf, Cf=0.577*racine(nu/u0/x), Cf=0.577/racine(Re). Le débit d'énergie cinétique déficitaire est W-=integrale[0,e](rho*u*(u0²/2-u²/2)*dy)=(rho*u0³/2)*integrale[0,e]((y/e-y³/e³)*dy), W-=(rho*u0³/2)*(e/2-e/4), W-=(rho*u0³*e/8), W-=Pdyn*u0*e/4 (en W/m). On aurait pu l'utiliser pour calculer e, ce qui donne une c.l. 15% plus épaisse (c'est une légère contradiction du modèle). Le coefficient de frottement global Cfg est défini par P-(x0)=Pdyn*Cfg*x0 au point x0. Il est adimensionnel. On a cfg=(1/x0)*integrale[0,x0](Cf*dx)=(1/x0)*racine(nu/u0)*0.577*integrale[0,x0](dx/racine(x))=1.155*racine(x0*nu/u0), Cfg=1.155/racine(Rex0). Cfg est donc 2 fois plus élevé que Cf. Cette estimation est 13% moins élevée que celle de Blasius (Cfg=1.328/racine(Rex0) voir résultats expérimentaux ), laquelle est en accord quasi-parfait avec les mesures de Nikuradse. On peut donc considérer notre modèle satisfaisant, car il est beaucoup plus simple à transposer (tout se calcule à partir du paramètre e, l'épaisseur de couche). |
||||||||||||||||||||||||||||||||||||||||||||||
Quand le nombre
de Reynolds Re, proportionnel à x, passe la valeur 4.85e5
(environ),
la couche limite devient turbulente avec une sous-couche laminaire.
Nous
n'étudierons pas la couche limite turbulente car naturellement
instable
et sensible à toutes sortes d'influences (vibrations, ondes
sonores
etc..) elle résiste à la modélisation et en plus
elle
est source de frottements supplémentaires, ce que, à
isentropics.org,
nous préférons éviter. Si certains la
préfèrent,
c'est qu'elle résiste mieux au décollement de veine, mais
on peut obtenir le même résultat par absorption partielle
de la couche limite laminaire (voir décollement
de veine ). |
||||||||||||||||||||||||||||||||||||||||||||||
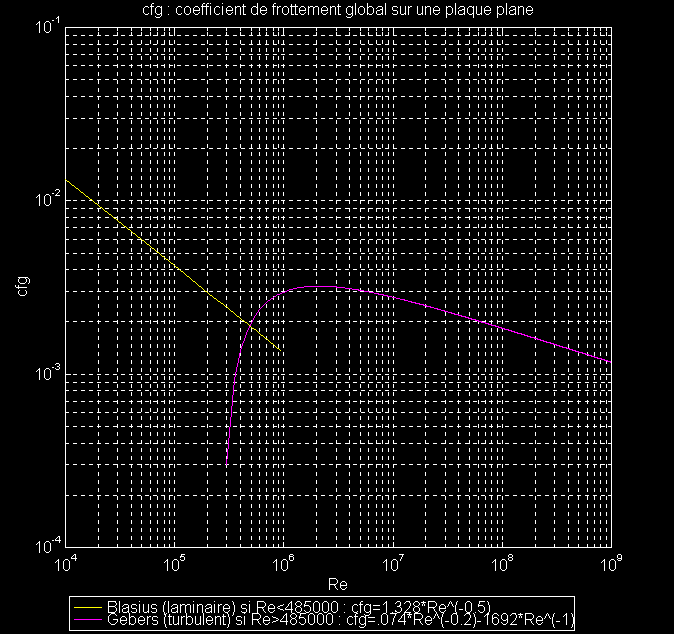 Voici
les résultats expérimentaux concernant le Cfg: la valeur
vraie est la plus grande des 2. Pour Re=4.85e5 une transition se
produit,
assez brusque. En turbulent on peut extraire le coefficient de
frottement
local Cf par dérivation du Cfg :
Cf(x)=d(x*Cfg)/dx=Cfg+x*d(Cfg)/dx, Cf(x)=Cfg+x*[d(Re)/dx]*[d(Cfg)/d(Re)], Cf(x)=Cfg+Re*[d(Cfg)/d(Re)] , Cf(x)=5.92e-2*Re^(-0.2). Chose étrange, le terme en Re^(-1) disparaît. Il correspond à un frottement local nul (si l'on arrête tout frottement à partir d'une abcisse donnée, le Cfg baisse en 1/Re). Pour Re=4.85e5, Cf(laminaire)=1.9e-3, Cf(turbulent)=4.32e-3, soit une multiplication par 2.3, équivalant à une division par 2 de la sous-couche laminaire. |
||||||||||||||||||||||||||||||||||||||||||||||
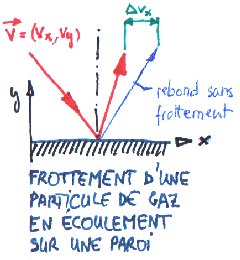 Vitesse
nulle à la paroi ?
La contrainte tangentielle de frottement sur la paroi est l'effet des molécules de gaz qui lui cèdent une partie de leur impulsion horizontale m*Vx, où m est la masse de la molécule. Si la vitesse moyenne <Vx> est nulle à la paroi (hypothèse communément admise), les molécules heurtent la paroi en moyenne perpendiculairement, donc elles rebondissent en moyenne perpendiculairement, l'impulsion transmise est nulle et donc la contrainte de frottement est nulle, ce qui est faux. Par conséquent l'hypothèse de vitesse nulle à la paroi est invalide. Il nous faut donc calculer <Vx> en relation avec la contrainte de frottement tau. On s'aidera du modèle de frottement coulombien (solide sur solide) représenté dans la figure ci-dessous. |
||||||||||||||||||||||||||||||||||||||||||||||
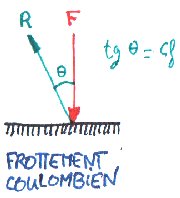 Dans
le modèle
du frottement de Coulomb, un solide appuie sur un autre avec la force
normale
(perpendiculaire à la surface de contact) F. La
réaction
R
(force exercée par la surface sur le solide) est
indépendante
de la superficie de contact et ne dépend que de F et d'un
coefficient
de frottement solide Cfs caractéristique des 2
matériaux:
R=(Rx,Ry)=F*(-Cfs, 1) avec Cfs=0.3 (acier-acier), Cfs=0.1 (acier-acier
lubrifié), Cfs=0.04 (le minimum, téflon sur tous
matériaux),
Cfs=1 à 4 (le maximum, gomme sur solides). R s'oppose au
glissement.
Cfs a tendance à diminuer avec la vitesse de glissement, ce qui
peut induire un
broutement.
Le modèle de Coulomb est un modèle macroscopique. Pour le transposer aux gaz, nous devons en trouver un équivalent microscopique. C'est ce que fait la figure ci-dessous. |
||||||||||||||||||||||||||||||||||||||||||||||
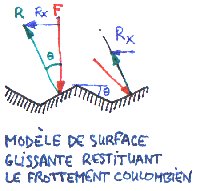 Une
surface
glissante (Cfs=0) avec des stries microscopiques dont les faces font
avec
le plan de glissement un angle têta=arctg(Cfs) se comporte au
niveau
macroscopique comme une surface de coefficient de frottement Cfs.
L'avantage est que nous pouvons maintenant calculer le choc d'une molécule de gaz sur la paroi. Si u est la vitesse à la paroi, Pdyn=(rho*u²/2) la pression dynamique, la pression exercée sur le versant frontal est Pf=P+Pdyn*sin(têta) et sur le versant fuyant Pf'=P-Pdyn*sin(têta). La pression moyenne est donc P et la contrainte tangentielle tau=Pdyn*sin(têta)*tg(têta)=Pdyn*cos(têta)*tg²(têta). Comme tg²+1=1/cos², tau=Pdyn*Cfs²/racine(Cfs²+1). Quand Cfs est petit devant 1, on peut approximer u(y=0)=racine(2*tau/rho)/Cfs. Comme tau=eta*du/dy=eta*u' (eta en Pa.s, viscosité dynamique), il vient Cfs²*u²=2*eta*u'/rho, (1/u)'=-u'/u²=-rho*Cfs²/(2*eta), (1/u)'y=0=-Cfs²/(2*nu), Cfs et nu ne dépendent que de la paroi et de (T,P) du fluide et donc (1/u)', qu'on appelle gradient de lenteur à la paroi, peut être calculé en tout point sans connaître le profil des vitesses et est d'ailleurs constant le long de la paroi. A titre d'exemple, pour de l'air à 300K et 1 bar, nu=1.55e-5 m²/s, et pour de l'acier Cfs=0.3, donc (1/u)'=-2900 s/m². Si l'écoulement est sonique (u0=300m/s) et l'écoulement à la limite de la transition turbulente (nombre de Reynolds Re=4.85e5, avec Re=u0*x/nu, donc x=25mm et e=0.124mm, rho=1.2, eta=1.86e-5, tau=45 Pa), u(y=0)=28.9 m/s soit 10% de la vitesse d'écoulement, ce qui est à la limite du négligeable. Par contre si la paroi est en téflon (Cfs=0.04), alors u(y=0)=216 m/s (72% de la vitesse générale!). L'approximation de vitesse nulle à la paroi ne colle plus du tout à la réalité et il faut recalculer toute la couche limite... ce cas est très interessant car il permet de réaliser des microéjecteurs à débit sonique qui communiquent très vite leur impulsion à un flux sans avoir trop de pertes. |
Quand un écoulement
frotte sur une paroi, il se forme une couche de fluide ralenti au
voisinage
de cette paroi, qu'on appelle couche limite et de laquelle
dépendent
de nombreuses propriétés de l'écoulement
(frottement,
transferts thermiques et décollement éventuel de
l'écoulement).
La figure ci-contre représente le profil des vitesses u(y)
à différentes abcisses x (distance au début de la
plaque). On considère que la couche limite est en
équilibre
de pression avec la veine fluide, ce qui est vrai avant l'apparition de
la turbulence.