VENTURIS ET COLS SONIQUES ...

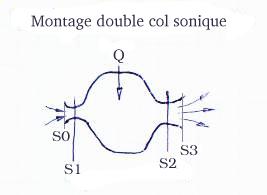Montage double col soniqueMontage double col sonique: on étudie le montage suivant: une capacité raccordée à 2 goulots où l'écoulement de l'air est à la vitesse du son. Ces cols soniques, de sections de passage S1 et S2, sont supposés parfaits (sans perte de pression). S0 est la section d'entrée convergent, S3 la section de sortie du divergent (ou du décollement de veine s'il a lieu). La vitesse de l'air est à peu près nulle dans la cavité, à laquelle on fournit un flux de chaleur Q. La pression atmosphérique est P, le débit massique M.
Que se passe-t-il ?

  • BdSV: 1+ 0.2025*mach²=(Ti/T)=(Pi/P)0.288 =(rhoi/rho)0.405=(ai/a)², avec mach=u/a=1

    • on en tire T1/Ti1=T2/Ti2=0.832, P1/Pi1=P2/Pi2=0.527, rho1/rhoi1=rho2/rhoi2=0.634, u1²=403*T1, u2²=403*T2.
    D'autre part, si M est le débit massique, cp la capacité thermique massique isobare de l'air (1005 J/kg/K), Q=M*cp*(Ti2-Ti1)=M*cp*(Ti3-Ti0)=M*3*(u2²-u1²), Ti0=Ti1 et Ti2=Ti3, M=Sj*rhoj*uj quelquesoit j dans {1..4}.
    Donc Q=1208*M*(T2-T1)=1208*(S2*rho2*u2*T2-S1*rho1*u1*T1), Q=4.209*(S2*P2*u2-S1*P1*u1)=2.218*(S2*Pi2*u2-S1*Pi1*u1). Comme Pi2=Pi1, Q=2.218*(S2*Pi2*u2-S1*Pi1*u1)=2.218*Pi1*(S2*u2-S1*u1)=2.218*Pi1*u1*(S2*(1+racine(Q/3/M))-S1). Enfin S2=S1+Q/(2.218*Pi1*u1)/(1+racine(Q/3/M)) (relation entre S1,S2 et Q).

    Calcul de la poussée F:
    Si F0 et F3 sont les débits d'impulsion en S0 et S3, F0=P0*S0+M*u0, F=F3-F0=(P3-P)*S3-(P0-P)*S0+M*(u3-u0).
    Arrivé à ce point, une question se pose, récurrente dans tous les problèmes de jet: faut-il considérer P3=P ou bien Pi3=P ?

  • Une chose est sûre: Pi3>=P, sans quoi le flux de matière va s'inverser. Considérant uniquement le col de sortie, P3 n'admet pas de limite supérieure. Simplement si P3>P, le jet va s'évaser en sortie. 
  • Si Pi3>P>P3, le jet libre va s'écraser latéralement sous l'effet de la pression extérieure P, son impulsion F(x)=P(x)*S(x)+P*[S3-S(x)]+M*u(x) restant constante tant qu'on néglige l'effet de la viscosité. On a donc [P(x)-P]*S(x)+M*u(x) constant, puis en notant d'un indice f les conditions finales du jet, M*uf=M*u3+[P3-P]*S3, uf-u3=(P3-P)*S3/M < 0. Passé S3, la vitesse baisse donc, la section diminue, tandis que la pression augmente, ce qui est surprenant car dans une tuyère en écoulement isentropique, quand la section diminue, la vitesse augmente, et la pression diminue. On doit donc supposer qu'une telle situation est impossible, et que P3=P. Pour des raisons similaires, P0=P.
  • Alors F=M*(u3-u0). Comme Pi0=Pi1 et Pi2=Pi3, que les cols 1 et 2 sont soniques, on peut calculer u0 et u3 itérativement par la formule M/S=rhoi.u.[1-u²/(1990.Ti)]^2.47 (tirée de BdSV, valable pour l'air) et donc la poussée F.



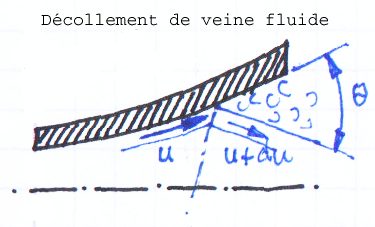    • décollement de veine fluideDécollement de veine (dit aussi de couche limite, ou décrochage sur un profil d'aile): 
    Les décollements ont lieu dans les sections divergentes (et jamais dans les convergents).
    On considère une couche fluide d'épaisseur e longeant la paroi à la vitesse u0. Sa pression est P0 tandis qu'à l'aval du décollement la pression est P1 et la vitesse nulle. Appelons têta l'angle du décollement. Effectuons le bilan des forces le long de la ligne de décollement:
    P0+rho.(u0.sin(têta))²/2=P1 donc sin(têta)=racine(2(P1-P0)/rho)/u0. Il peut y avoir décollement si P1>P0. Le décollement est d'autant plus fort que u0 est faible: si la couche limite est épaisse,le point de décollement sera plus en amont. Le cas sin(têta)>1 correspond à P1>Pi0. Le flux est alors bloqué et une onde de choc (coup de bélier) remonte vers l'amont. C'est une situation instable, non étudiée ici. Notons que le flux aval n'est pas nécessairement convergent comme sur la figure.
    Appelons Pi0=P0+rho.u²/2 la pression d'impact. On en tire sin²(têta)=2(P1-P0)/(rho.u0²)=1+2(P1-Pi0)/(rho.u0²)=1-(Pi0-P1)/(Pi0-P0)=1-cos²(têta), puis cos(têta)=racine[(Pi0-P1)/(Pi0-P0)]
    Cette formule permet de calculer l'angle du décollement mais pas sa position. Quand têta est faible toutefois, la zone stagnante est chassée par les forces viqueuses: P1 diminue vers la pointe de l'angle. A une distance x derrière le point de décollement, la contrainte visqueuse est tau=µ.u0/(têta.x), (µ est la vicosité dynamique, 17e-6 Pa.s pour l'air à 20°C) égale au gradient des forces de pression têta.x.d(P1)/dx. Donc d(P1)=-(µ.u0/têta²).d(1/x) : en intégrant jusqu'à x=0 on obtient une baisse de P1 infinie, donc pas de décollement. Cette formulation montre que la couche limite joue un rôle fondamental (en son absence pas de décollement).
    Considérons une couche limite simplifiée d'épaisseur y, dans laquelle u varie linéairement de 0 à u0. Corrigeons un peu les formules ci-dessus: tau=µ.u0/(y+têta.x)=(y+têta.x).d(P1)/dx, donc d(P1)=-µ.u0/(y+têta.x)².dx=-(µ.u0/têta).d(1/(y+têta.x)).
    Il suffit de pousser l'intégration jusqu'à x=0. En appelant Pf la pression en fin de tuyère ou de profil, et xf l'abcisse de sortie de tuyère (ou de fin de profil), il vient P1=Pf-(µ.u0/têta).[(1/y)-(1/(y+têta.xf))]. En approximant têta à sin(têta), on trouve têta²=1+2(Pf-Pi0-(µ.u0/têta).[1/y-1/(y+têta.xf)])/(rho.u0²), mais le plus intéressant est de trouver l'ensemble des lieux où têta=0 (la zone non décollée) et plus particulièrement sa borne inférieure en xf. Sur cet ensemble, P1<P0, donc Pf-P0<(µ.u0/têta).[1/y-1/(y+têta.xf)]. P0 et u0 sont liés: Pi0=P0+rho.u0²/2, puis Pf-Pi0<(µ.u0/têta).[1/y-1/(y+têta.xf)]-rho.u0²/2, qui donne 2 cas particuliers interessants:
  • Quand têta est grand, Pf-Pi0<µ.u0/(têta.y)-rho.u0²/2. 
  • Quand têta=0, Pf-Pi0<µ.u0.xf/y²-rho.u0²/2.
  • Le pire têta est celui qui réalise le minimum de F=[1/y-1/(y+têta.xf)]/têta. Comme dF/d(têta)=-xf²/[y.(y+têta.xf)²] ne s'annule que pour têta=infini, on retombe dans le 1er cas. On voit que la condition de décollement est plus facilement atteinte quand têta est grand, ce qui explique que les décollements soient des phénomènes brusques.

    • Pour éviter tout décollement de veine, il faut respecter ces 2 inéquations, qui se ramènent à une seule si l'on pose A=max(têta,y/xf). Alors Pf-Pi0<µ.u0/(A.y)-rho.u0²/2, puis (rho/2).u0²-µ.u0/(A.y)+Pf-Pi0<0 (condition de chasse). (y/xf) est généralement petit devant un têta de décollement, sauf en fin de tuyère, où il y a donc toujours un décollement si la pression extérieure n'est pas atteinte: une jupe souple en fin de tuyère peut diminuer ce problème.
    Dès que xf > 4.y, on peut approximer P1=Pf-µ.u0/(têta.y), puis têta²=1-(Pi0-Pf)/(rho.u0²/2) + 2.µ/(têta.y.rho.u0). Une condition suffisante de recollement est 2.µ/(têta.y.rho.u0) > 1, soit têta < 2.µ/(y.rho.u0), puis Pi0-Pf >= rho.u0²/2 - 2.µ²/(y².rho). Si M est le débit-masse, constant sur toute la tuyère, S la section locale (m²), Pi0-Pf >= (1/rho).(M²/(2.S²) - 2.µ²/y²). Pour être tranquille, on peut choisir 
    y <= 2.µ.S/M (épaisseur de couche limite anti-décollement), qu'on peut gérer par absorption de la couche limite à travers la paroi. Pour un profil d'aile on préfèrera la formule y <= 2.µ/(rho.u), où rho et u sont la densité et la vitesse relative de l'air loin du profil.

    écoulement radialÉcoulement radial divergent compressible: 



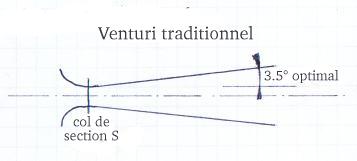    venturi traditionnelVenturi traditionnel: Le venturi est un organe déprimogène: quand un débit le traverse, il apparaît une baisse de pression au col proportionnelle au carré du débit. On peut s'en servir comme mesure de débit, aération de l'eau par injection d'air au niveau du col, mélangeur air-fuel de précombustion, en régulateur de débit (le débit maximum pour de l'air est obtenu quand la vitesse au col est la vitesse du son, pour de l'eau quand la pression statique au col est la pression de vapeur saturante: en variant la section du col, on varie le débit pour une pression amont donnée). De nombreux éjecteurs sont conçus avec une buse d'éjection juste en amont du col d'un venturi. On verra plus bas une application inédite, le venturi propulsif.

    Les dimensions d'un venturi sont fixées par une norme, la norme AFNOR NFX-10101. Cette norme fixe les dimensions suivantes:

  • angle d'ouverture convergent = 21° (non conforme au dessin ci-contre)
  • longueur du col = d (d diamètre du col)
  • angle d'ouverture divergent entre 7° et 30° (cet angle est donné à titre indicatif, il intervient seulement sur la perte de pression du dispositif).

    • Ces dimensions sont données pour faciliter son étalonnage en tant que débitmètre, mais ce qui nous intéresse ici, c'est plutôt son coté tuyère convergente-divergente. 
    perte de charge non récupérable en % de la pression différentielle
    d/D 0 0.1 0.2 0.3 0.4 0.6 et +
    % 25 18 13 10 8 5

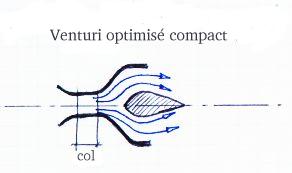    venturi optimisé compactVenturi optimisé compact: La présence d'un noyau permet d'accélerer l'élargissement de la section dans le divergent sans toutefois engendrer un décollement de veine.



    venturi propulsifVenturi propulsif: Ç'est la dépression au col qui crée le débit et non l'inverse comme dans un venturi classique. Ça fonctionne si l'angle du convergent est plus grand que celui du divergent, mais peut on ainsi atteindre la vitesse du son au col ? La pression statique en sortie de tuyère doit être égale à la pression ambiante pour éviter un décollement de veine. La pression statique à l'entrée du convergent doit être inférieure à la pression ambiante Donc la section d'entrée doit être inférieure à la section de sortie. L'impulsion motrice est donnée par l'absorption de la couche limite amont et des gaz lents.



    question?
    INDEX