 Ceci représente au choix :
Ceci représente au choix :
dFu=rho/2.c.dr.v(cz.w-cx.u)=traction locale (en r, sur la longueur dr) dFw=rho/2.c.dr.v(cz.u+cx.w)="traînée" locale (en r, sur la longueur dr) PP=somme(u.dFu), où somme représente l'intégrale pour r variant de 0 à R. PF=-somme(w.dFw). Comme v=sqrt(u²+w²)=sqrt(u²+omega².r²), PP=rho/2.somme(u.c.dr.sqrt(u²+omega².r²).(cz.omega.r-cx.u)) On a vu sur la page de la caudale que b, proportionnel à r, ne peut donc être optimal partout. Pour le voilier, on cherche à maximiser la composante de la force dans la direction souhaitée, faisant un angle t avec w, la dérive ou la quille du dit voilier permettant d'extraire la composante souhaitée Ft de la résultante F.... |
|
 Ceci représente au choix :
Ceci représente au choix :
Les éjecteurs ont fait leurs preuves en tant que pompes à vide, par leur large gamme de pressions de fonctionnement, leur simplicité et leur fiabilité. Quelques fabricants: smc-france, kinetics-therm, etc... |
|
 Voici le détail de la sortie d'éjecteur sur lequel nous allons
établir le modèle. On l'a coupé aux axes de symétrie.
Voici le détail de la sortie d'éjecteur sur lequel nous allons
établir le modèle. On l'a coupé aux axes de symétrie.
On fait le calcul en considérant que les 2 fluides HP et BP sont des gaz parfaits, à savoir de l'air. On note S les sections de passage, P les pressions statiques, T les températures absolues, M les débits massiques, rho les masses volumiques, F les forces, E les puissances, V=(Vx,Vy) les vitesses locales, a les vitesses du son, K les entropies (K=cp*ln(T)-r*ln(P)), 0x l'axe longitudinal, 0y l'axe transversal. Un indice i correspond à une condition d'impact (d'arrêt). Les conditions en 2 sont supposées connues (c'est le fluide à compresser). Voilà 11*3=33 paramètres. On voit que S1+S2=S3+S4 =Stotale ainsi que Vy2=Vy3=Vy4=0, Vy1 non constant sur toute la largeur, est à déterminer. Par conservation de la masse, M1=M3 et M2=M4. On pose M=M1+M2. Par conservation de l'impulsion (quantité de mouvement), F1+F2=F3+F4. Par conservation de l'énergie, E1+E2=E3+E4. Pour un éjecteur idéal (isentropique) K1=K3 et K2=K4. En sortie on a équilibre des pressions: P3=P4 et des vitesses: Vx3=Vx4 Nous voilà donc avec 11 équations. D'autre part quelquesoit j dans {1..4} soit 7*3=21 équations de plus, soit 32 en tout, pour 33 inconnues, et l'écoulement est déterminé si on choisit P4. Fixons donc la pression de sortie P4. On appelle W la puissance mécanique transmise (du fluide1 au fluide2) et Q la perte exergétique (Q=0 à l'idéal et pour une 1ère analyse). Par commodité appelons D (pour déflexion) le rapport (Vy1/Vx1) Connaissant (M,E,F,V)j on peut retrouver (rho,T,P,S)j avec les équations ci-dessus. On s'attachera donc à identifier (M,E,F,Vx,Vy)j. Qualitativement, le fluide 1 exerce sur le fluide 2, le long de la ligne en pointillé, (BdSV=Barré de Saint-Venant : gaz parfait (air) en évolution isentropique sans apport de travail, dans un écoulement stationnaire monodimensionnel) Les conditions d'impact en 2 sont données, ce sont celles du réservoir amont. Par contre les conditions en 1 sont à optimiser, car le fluide 1 est un moyen de compression. On considère que S2 est donné, S1 à adapter. Comme le fluide 2 est destiné à être compressé, toute son évolution doit rester sonique ou supersonique, sans quoi une onde de pression va se propager vers l'amont, réduisant le débit M2. Supersonique n'est pas très intéressant, car On choisit donc l'écoulement sonique (avec apport de travail) dans toute l'évolution 2->4. Voyons donc les équations caractéristiques de ce type d'écoulement. BdSV ne marche plus le long de la ligne de courant, mais seulement en chaque point, entre conditions d'impact et conditions statiques. dW=M*dPi/rhoi est une formule équivalente. donc dQ=M*(cp*dT-dP/rho) On vérifie que dE=dW+dQ: dE=M*cp*dTi=M*(cp*dT + d(u²/2))=M*(cp*dT-dP/rho+dP/rho+d(u²/2))=dQ+dW. L'égalité est respectée, OK. Donc si dW>0 et dQ=0, cp*dT=dP/rho, dW=M*(dP/rho + d(u²/2))=M*(cp*dT + 201.5*dT)=1206.5*M*dT=dW La quantité de travail fourni qui passe sous forme cinétique est dWcin=M*d(u²/2)=201.5*M*dT, soit 17%, le reste (83%) passant sous forme de compression. En passant si dW=0 et dQ>0 (ce n' est pas le cas ici), -dP/rho=d(u²/2), dQ=M*(cp*dT+d(u²/2))=M*(cp*dT+201.5*dT)=1206.5*M*dT. L'augmentation d'énergie cinétique M*d(u²/2)=201.5*M*dT est la même (17%) qu'en apportant du travail, mais elle est cette fois-ci fournie par la détente de l'air. On a donc dW>0, dQ=0. On considère que l'écoulement du fluide 2 est isentropique (pas d'apport de chaleur, et on néglige pour l'instant la création d'entropie visqueuse). On en tire dP/P=3.5*dT/T, d(rho)/rho=2.5*dT/T, du/u=0.5*dT/T, dS/S=-3*dT/T.
|
|
 Voici le modèle d'écoulement qui a servi de base au calcul
de l'échangeur
thermique compact. Les courbes isothermes et isotaches (=isovitesses)
sont superposées, car les lois de transfert thermique et cinétique
sont similaires, linéaires, et les conditions aux limites ( pourtour
à valeur constante et gradient nul au centre ) identiques, à
une loi affine près. On est en régime stationnaire et laminaire,
donc les effets d'inertie n'interviennent pas. On sait que dans ces conditions,
on peut utiliser le concept de transformation conforme (qui transforme
un réseau à mailles carrées en réseau à
mailles carrées) du disque en carré. Les isothermes du cercle
sont alors transformées en isothermes du carré. La formulation
parabolique est valable si l'on prend y sur l'axe horizontal ou vertical
de la figure du haut ( x est l'axe de l'écoulement ). La notion
de diamètre hydraulique, qui donne l'effet d'échelle, est
approximative, et exacte uniquement dans le cas du tube rond. Il y a de
plus ici un deuxième problème de conduction de la chaleur
dans la paroi, qu'on résoud par l'addition des résistances
thermiques du fluide et de la paroi. Tous comptes faits, on est à
10-15% près sur les proportions (flux thermique)/(écart de
température fluide-axe.paroi) et (perte de charge (=de pression)
métrique)/(débit), dans le même sens, ce qui est suffisant
en l'occurence pour préferer s'occuper d'autre chose.
Voici le modèle d'écoulement qui a servi de base au calcul
de l'échangeur
thermique compact. Les courbes isothermes et isotaches (=isovitesses)
sont superposées, car les lois de transfert thermique et cinétique
sont similaires, linéaires, et les conditions aux limites ( pourtour
à valeur constante et gradient nul au centre ) identiques, à
une loi affine près. On est en régime stationnaire et laminaire,
donc les effets d'inertie n'interviennent pas. On sait que dans ces conditions,
on peut utiliser le concept de transformation conforme (qui transforme
un réseau à mailles carrées en réseau à
mailles carrées) du disque en carré. Les isothermes du cercle
sont alors transformées en isothermes du carré. La formulation
parabolique est valable si l'on prend y sur l'axe horizontal ou vertical
de la figure du haut ( x est l'axe de l'écoulement ). La notion
de diamètre hydraulique, qui donne l'effet d'échelle, est
approximative, et exacte uniquement dans le cas du tube rond. Il y a de
plus ici un deuxième problème de conduction de la chaleur
dans la paroi, qu'on résoud par l'addition des résistances
thermiques du fluide et de la paroi. Tous comptes faits, on est à
10-15% près sur les proportions (flux thermique)/(écart de
température fluide-axe.paroi) et (perte de charge (=de pression)
métrique)/(débit), dans le même sens, ce qui est suffisant
en l'occurence pour préferer s'occuper d'autre chose.
diamètre hydraulique=diamètre thermique=4*section/périmètre On en tire les 2 formules de travail:
|
|
|
dictionnaire en ligne des mots de la combustion formules élémentaires de MdF ( par rapport à cette page, des formules à l'échelle de la particule fluide ) Model Rocket Drag Analysis on apprend beaucoup de choses en peu de temps. Quoique le centre d'intérêt soit différent, bien dans l'esprit des écoulements standards |
|
|
|
|
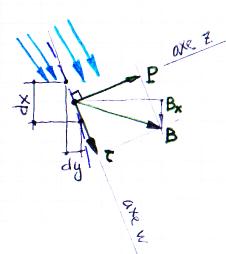 Pour aller plus loin, nous avons besoin de comprendre ce qui se passe à
la ligne de contact. Sur la figure ci-contre, on a créé 2
axes w et z alignés sur les vitesses et la surface de contact. P
est la pression locale, tau=-µ*(du/dz) la contrainte visqueuse (µ=4.697e-8*(T+76)
Pa.s étant la viscosité de l'air). Le fluide 1 exerce donc
sur le fluide 2 une force B*dw, avec dw²=dx²+dy², B=(tau,P)
dans le repère (w,z), B=(Bx,By) dans le repère (x,y), dw=(dx,dy)(x,y),
dz=(-dy,dx)(x,y), B*dw=(tau*dw,P*dw)(w,z)=(tau*dx-P*dy,tau*dy+P*dx)(x,y)
Pour aller plus loin, nous avons besoin de comprendre ce qui se passe à
la ligne de contact. Sur la figure ci-contre, on a créé 2
axes w et z alignés sur les vitesses et la surface de contact. P
est la pression locale, tau=-µ*(du/dz) la contrainte visqueuse (µ=4.697e-8*(T+76)
Pa.s étant la viscosité de l'air). Le fluide 1 exerce donc
sur le fluide 2 une force B*dw, avec dw²=dx²+dy², B=(tau,P)
dans le repère (w,z), B=(Bx,By) dans le repère (x,y), dw=(dx,dy)(x,y),
dz=(-dy,dx)(x,y), B*dw=(tau*dw,P*dw)(w,z)=(tau*dx-P*dy,tau*dy+P*dx)(x,y)
 La relation tau=1.2*S*dP/dx devrait nous donner une 2ème relation
entre tau, P et S' .
La relation tau=1.2*S*dP/dx devrait nous donner une 2ème relation
entre tau, P et S' .